With the unfortunate news over the weekend of the passing of famed Princeton Mathematician John Conway, I thought of his famous “Game of Life” and how it has always been a fascinating illustration of how even from rigid structure and rules, amazing complexity can emerge.
What is the Game of Life?
The Game of Life is not a “game” in the usual sense. It is “played” on an infinite grid with some cells initially shaded, but everything is determined from this starting position (there is no choice involved). A set of simple rules dictate which cells become shaded or unshaded at each step. Then everything repeats. (In this way, the Game of Life is more accurately referred to as a “cellular automaton.”)
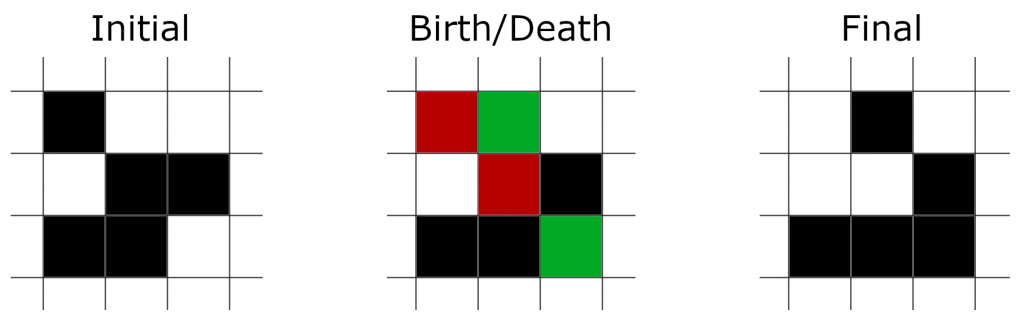
Every cell’s behavior is determined by it’s eight neighbors (four sides and four diagonals). Following the name, a shaded cell is living and an unshaded cell is dead.
- A living cell with exactly two or exactly three neighbors continues living.
- A living cell with less than two or more than three neighbors dies. (We’ll refer to this as death.)
- A dead cell with exactly three neighbors becomes alive. (We’ll refer to this as birth.)
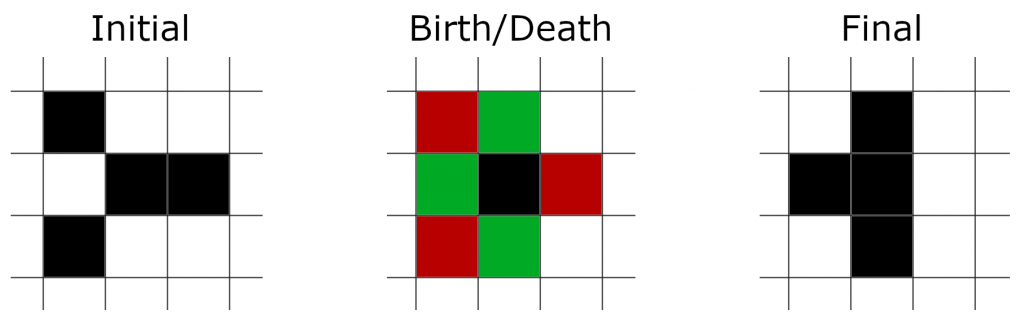
Despite the simple rules, different initial conditions can lead to very different behaviors. Some initial positions are static and never change, such as a 2×2 square. Many positions grow forever or eventually lead to a blank board (everything dies). Others lead to a simple repeating pattern.

The best way to see the power of the Game of Life is experiment yourself! There are many implementations online or available for download. One such implementation is available at playgameoflife.com/. Try out your own starting positions, or try one of the starting positions that come pre-programmed, such as the glider.
Why is the Game of Life Relevant?
John Conway is famous for a lot of different things in mathematics, and admittedly the Game of Life is not the most advanced mathematically. That being said, it is a great introduction to the idea that complex behaviors can come from simple initial conditions. It also shows the importance of those initial conditions. For example, the two examples shown above differ by a single shaded cell, yet their end behaviors are very different. Lastly, it serves as an easy exposure to programming, which at its core is simply a set of instructions that need to be followed.
New and interesting patterns and initial conditions are being discovered to this day, try some out and share your favorites. Have a different result or idea inspired by John Conway that is your personal favorite? Please share that as well!
Share this post!