Sometimes the simplest math questions turn into hard math problems at the slightest overlook of how a question is structured. There are many of these odd questions circulating around the internet that many often think they have the answer to right off the bat, but under further investigation we are tricked! Read below and see for yourself how these problems get tricky.
A Bat and a Ball, So What?
A baseball bat and a baseball cost 1.10 together. The bat costs a dollar more than the ball. At first instinct you’d think this problem is a closed case with the ball costing 10 cents and the bat costing a dollar, right?
Nope.
The ball costs 5 cents! Remember, the bat costs a dollar more than the ball, and if the ball costs 5 cents with the bat a dollar more, it makes sense that the ball would cost 5 cents and the bat 1.05 dollars. Whoops! Sometimes even the simplest of problems are actually hard math problems!
Parentheses, Exponents…What Then?
Just like our featured image for today, this math problem is difficult because it matters in the way we interpret PEMDAS. You remember in high school, the poster in the corner with the green monster named PEMDAS? Yep, the order of operations applies here with this sneaky little problem:
6 / 2(1+2) = ?
The natural instinct is to add the digits in the parentheses first to 3, and then carry the two into the parentheses, making 6. Then, 6/6 = 1, right?
Nope.
Actually, the order of operations states that the multiplication and division aspects should be followed in the order of the equation, and not just multiplication first. The 2 in front of the parentheses might be a little distracting for many, and people tend to carry the two into the parentheses first. The actual answer to this is 9, if followed properly. Did it fool ya? It fooled many others!
If Half of 5 is 3, then…Huh?
We don’t want to spoil too much of this next brain-bender, but you probably guessed what the problem is already.
If half of 5 is 3, then what is one-third of 10?
Ouch. The gears are turning, but they’re almost grinding to a halt. This hard math problem can be solved if you think you have to round up to 3. If that’s the case, the problem seems a lot simpler once you “round up” a third of 10…to 4.
There are, interestingly enough, different ways to do this problem with different results. However, the most accepted answer is 4. Is that what you got?
We’re Areteem. Thanks for reading. Contact us to learn more of what we’re about.
Share this post!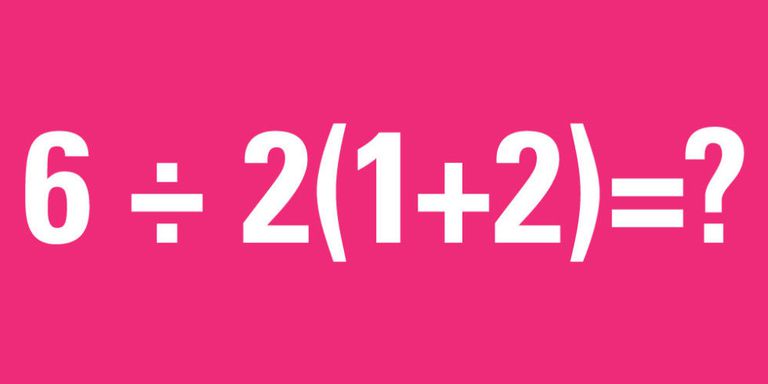
If “half of 5 is 3”, you can say anything about “1/3 of 10”. Logically, based on a false premise, any conclusion is possible.
There is a story about the famous logician, Bertrand Russell. In a lecture on logic, Russel mentioned that in the sense of material implication, a false proposition implies any proposition.
A student raised his hand and said “In that case, given that 1 = 0, prove that you are the Pope.”
Russell immediately replied, “Add 1 to both sides of the equation: then we have 2 = 1. The set containing just me and the Pope has 2 members. But 2 = 1, so it has only 1 member; therefore, I am the Pope.”